
Progressão geométrica
Entenderemos por progressão geométrica ou PG como qualquer seqüência de números reais ou complexos, onde cada termo a partir do segundo é igual ao anterior, multiplicado por uma constante denominada razão.
Exemplo:
(1, 2, 4, 8, 16, 32,...) PG de razão 2
(5, 5, 5, 5, 5, 5, 5,...) PG de razão 1
(100, 50, 25,...) PG de razão 1/2
(2, -6, 18, -54, 162, ...) PG de razão -3
Classificação :
Crescente: q > 1 e a1 > 0; ou 0 <> 1 e a1 <> 0
Oscilante: q < q ="1" q =" 0" class="MsoListParagraphCxSpLast" style="text-indent: -18pt;">rmula do Termo Geral:
Seja a PG genérica: (a1, a2, a3, a4, ... , a n, ... ) , onde a1 é o primeiro termo, e an é o n-ésimo termo, ou seja, o termo de ordem n. Sendo q a razão da PG, da definição podemos escrever:
a2 = a1 . q
a3 = a2 . q = (a1 . q) . q = a1 . q2
a4 = a3 . q = (a1 . q2) . q = a1 . q3
a) Dada a PG (2,4,8,... ), pede-se calcular o décimo termo.
Temos: a1 = 2, q = 4/2 = 8/4 = ... = 2. Para calcular o décimo termo ou seja a10, vem pela fórmula:
a10 = a1 . q9 = 2 . 29 = 2. 512 = 1024
Propriedade :
- Em toda PG, um termo é a média geométrica dos termos imediatamente anterior e posterior.
Exemplo:
PG (A,B,C,D,E,F,G)
Temos então:
B2 = A . C ;
C2 = B . D ;
D2 = C . E ;
E2 = D . F etc.
Soma dos n primeiros termos de uma PG
Seja a PG (a1, a2, a3, a4, ... , an , ...) . Para o cálculo da soma dos n primeiros termos Sn , vamos considerar o que segue:
Sn = a1 + a2 + a3 + a4 + ... + an-1 + an
Multiplicando ambos os membros pela razão q vem:
Sn . q = a1 . q + a2 .q + .... + an-1 . q + an .q .
Logo, conforme a definição de PG, podemos reescrever a expressão acima como:
Sn . q = a2 + a3 + ... + an + an . q
Observe que a2 + a3 + ... + an é igual a Sn - a1 . Logo, substituindo, vem:
Sn . q = Sn - a1 + an . q
Simplificando chegaremos à seguinte fórmula da soma:
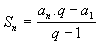
Se substituirmos a n = a1 . qn-1 , obteremos uma nova apresentação para a fórmula da soma, ou seja:
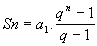
Exemplo:
Calcule a soma dos 10 primeiros termos da PG (1,2,4,8,...)
Temos:
Soma dos termos de uma PG INFINITA
Considere uma PG ILIMITADA ( infinitos termos) e decrescente. Nestas condições, podemos considerar que no limite teremos an = 0.
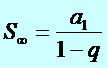
Exemplo:
Resolva a equação: x + x/2 + x/4 + x/8 + x/16 + ... =100
Ora, o primeiro membro é uma PG de primeiro termo x e razão 1/2. Logo, substituindo na fórmula, vem:
Daí, vem: x = 100 . 1/2 = 50
Calcule a soma dos 10 primeiros termos da PG (1,2,4,8,...)
Temos:
Soma dos termos de uma PG INFINITA
Considere uma PG ILIMITADA ( infinitos termos) e decrescente. Nestas condições, podemos considerar que no limite teremos an = 0.
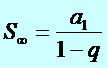
Exemplo:
Resolva a equação: x + x/2 + x/4 + x/8 + x/16 + ... =100
Ora, o primeiro membro é uma PG de primeiro termo x e razão 1/2. Logo, substituindo na fórmula, vem:
Daí, vem: x = 100 . 1/2 = 50


Nenhum comentário:
Postar um comentário